Modeling Irregularly Spaced Residual Series as a Continuous Stochastic Process

Abstract

Learning continuous-time stochastic dynamics is a fundamental and essential problem in modeling irregular time series, whose observations are irregular and sparse in both time and dimension. For a given system whose latent states and observed data are multivariate, it is generally impossible to derive a precise continuous-time stochastic process to describe the system behaviors. To solve the above problem, we apply Variational Bayesian method and propose a flexible continuous-time stochastic recurrent neural network named Variational Stochastic Differential Networks (VSDN), which embeds the complicated dynamics of the irregular time series by neural Stochastic Differential Equations (SDE). VSDNs capture the stochastic dependency among latent states and observations by deep neural networks. We also incorporate two differential Evidence Lower Bounds to efficiently train the models. Through comprehensive experiments, we show that VSDNs outperform state-of-the-art continuous-time deep learning models and achieve remarkable performance on prediction and interpolation tasks for irregular time series.

Keywords

Neural Stochastic Differential Equations
Stochastic recurrent neural network
Irregular time series

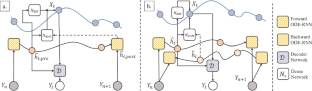
References

Archambeau, C., Opper, M., Shen, Y., Cornford, D., Shawe-taylor, J.S.: Variational inference for diffusion processes. In: Advances in Neural Information Processing Systems 20 (2008)

Google Scholar
Burda, Y., Grosse, R., Salakhutdinov, R.: Importance weighted autoencoders. ArXiv arXiv:1509.00519 (2016)
Burgess, C.P., et al.: Understanding disentangling in \(\beta \)-VAE (2018)

Google Scholar
Chen, T.Q., Rubanova, Y., Bettencourt, J., Duvenaud, D.K.: Neural ordinary differential equations. In: Advances in Neural Information Processing Systems vol. 31, pp. 6571–6583 (2018)

Google Scholar
Chung, J., Kastner, K., Dinh, L., Goel, K., Courville, A.C., Bengio, Y.: A recurrent latent variable model for sequential data. In: Advances in Neural Information Processing Systems, vol. 28, pp. 2980–2988 (2015)

Google Scholar
Cremer, C., Morris, Q., Duvenaud, D.: Reinterpreting importance-weighted autoencoders. In: International Conference on Learning Representations (ICLR) - Workshop Track (2017)

Google Scholar
De Brouwer, E., Simm, J., Arany, A., Moreau, Y.: GRU-ODE-Bayes: continuous modeling of sporadically-observed time series. In: Advances in Neural Information Processing Systems, vol. 32, pp. 7379–7390 (2019)

Google Scholar
Higgins, I., et al.: \(\beta \)-VAE: Learning basic visual concepts with a constrained variational framework. In: International Conference on Learning Representations (ICLR) (2017)

Google Scholar
Ionescu, C., Papava, D., Olaru, V., Sminchisescu, C.: Human3.6m: large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 36(7), 1325–1339 (2014)

Google Scholar
Kingma, D.P., Welling, M.: Auto-encoding variational bayes. In: International Conference on Learning Representations (ICLR) (2014)

Google Scholar
Li, X., Wong, T.K.L., Chen, R.T.Q., Duvenaud, D.: Scalable gradients for stochastic differential equations. In: 23rd International Conference on Artificial Intelligence and Statistics, pp. 3870–3882 (August 2020)

Google Scholar
Liu, Y., Xie, D., Wang, X.: Generalized boltzmann machine with deep neural structure. In: The 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), vol. 89, pp. 926–934 (April 2019)

Google Scholar
Martinez, J., Hossain, R., Romero, J., Little, J.J.: A simple yet effective baseline for 3d human pose estimation. In: IEEE/CVF International Conference on Computer Vision (ICCV) (2017)

Google Scholar
Rainforth, T., et al.: Tighter variational bounds are not necessarily better. In: Proceedings of the 35th International Conference on Machine Learning, pp. 4274–4282 (2018)

Google Scholar
Rubanova, Y., Chen, T.Q., Duvenaud, D.K.: Latent ordinary differential equations for irregularly-sampled time series. In: Advances in Neural Information Processing Systems, vol. 32, pp. 5321–5331 (2019)

Google Scholar
Sussillo, D., Józefowicz, R., Abbott, L.F., Pandarinath, C.: LFADS - latent factor analysis via dynamical systems. ArXiv arXiv:1608.06315 (2016)

Download references

Acknowledgments

This work has been supported by NSF OIA 2040599, NSF OIA 2134840 and DOE 38456.

Author information

Authors and Affiliations

Stony Brook University, Stony Brook, NY, 11794, USA

Yingru Liu, Yucheng Xing, Xuewen Yang, Xin Wang & Zhaoyue Chen
University of Rochester, Rochester, NY, 14627, USA

Jing Shi
Amazon Alexa AI, Sunnyvale, CA, 94089, USA

Di Jin
Ward Melville High School, East Setauket, NY, 11733, USA

Jacqueline Wu

Editor information

Editors and Affiliations

Sampoerna University, Jakarta, Indonesia

Dr. Teddy Mantoro
Kyungpook National University, Daegu, Korea (Republic of)

Minho Lee
Sampoerna University, Jakarta, Indonesia

Media Anugerah Ayu
Murdoch University, Murdoch, WA, Australia

Dr. Kok Wai Wong
Universitas Indonesia, Depok, Indonesia

Dr. Achmad Nizar Hidayanto

Rights and permissions

Copyright information

About this paper

Verify currency and authenticity via CrossMark

Cite this paper

Liu, Y. et al. (2021). Continuous-Time Stochastic Differential Networks for Irregular Time Series Modeling. In: Mantoro, T., Lee, M., Ayu, M.A., Wong, K.W., Hidayanto, A.N. (eds) Neural Information Processing. ICONIP 2021. Communications in Computer and Information Science, vol 1516. Springer, Cham. https://doi.org/10.1007/978-3-030-92307-5_40

Download citation

.RIS
.ENW
.BIB

DOI : https://doi.org/10.1007/978-3-030-92307-5_40
Published: 02 December 2021
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92306-8
Online ISBN: 978-3-030-92307-5
eBook Packages: Computer Science Computer Science (R0)

rileydarl1983.blogspot.com

Source: https://link.springer.com/chapter/10.1007/978-3-030-92307-5_40